Chapter 10
Analyzing Circuits with Positive Feedback - Oscillators
Gordon W. Roberts
Department of Electrical & Computer Engineering, McGill University
Prior to the discovery of the negative feedback principle, electronic engineers were using the principle of positive feedback to create circuits that oscillate. Such circuits were used to create sinusoidal or square-wave signal generators as reference signals for various communication and instrumentation applications. For the longest time, oscillator designers of single-loop positive feedback structures have relied on the observation made by Heinrich Barkhausen in 1921 where he claimed that the circuit would oscillate provided the loop gain is unity and the phase shift is zero or a multiple of 2p at the same time. This was essentially a single frequency point metric; convenient, often incorrect. In 1932, Harry Nyquist introduced the Nyquist Stability Criterion that is applicable to both negative and positive feedback systems. In fact, his theory was written from the perspective of a positive feedback system. In this chapter we shall investigate the stability of single-loop positive feedback circuits using the method of Nyquist. As first used by Nyquist, the critical point of encirclement will be -1+j0 instead of 1+j0. It is suggested that one read Chapter 9 on Analyzing Single-Loop Feedback Circuits before reading this chapter, as many of the terms and concepts are introduced there first.
|
(a) |
(b) |
|
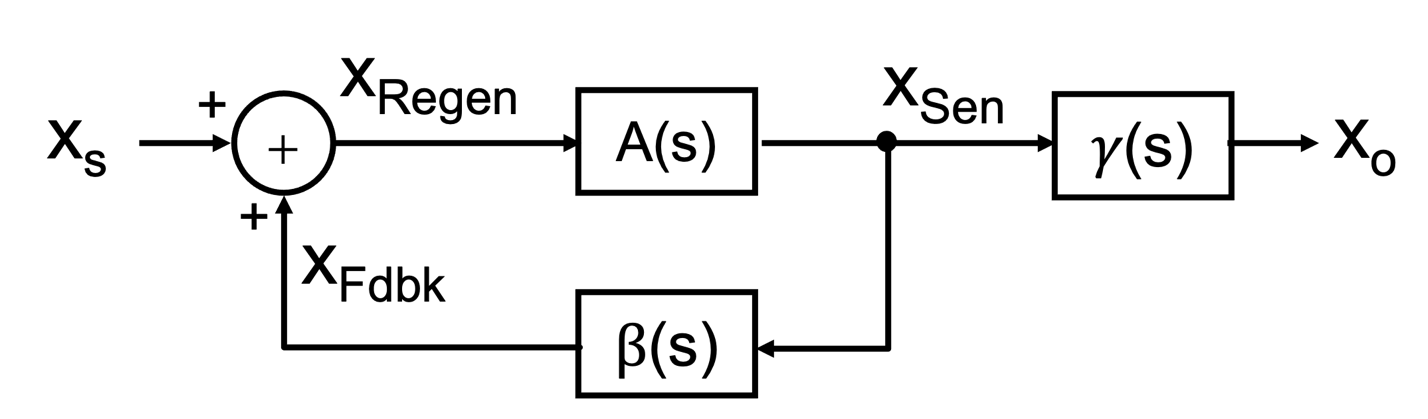
Fig. 10.1: The general form of a single-loop positive feedback structure: (a) classical structure, and (b) separating the sense signal from the output signal. |
|
10.1 The Single-Loop Positive Feedback Structure
The basic structure of a single-loop system including some form of positive feedback is shown in block diagram form in Fig. 10.1(a). Here the block depicted by A(s) represents the feedforward gain stage of the closed-loop system, and the block denoted by 𝛃(s) represents the feedback network. The summing node is used to add the feedback signal (xFdbk) that is fed back from the sensing signal with the input signal xs(s) to create what we shall call the regenerated signal xRegen(s). This regenerated signal is then applied to the input of the feedforward gain stage, thus creating the loop output sensing signal, xSen(s). The closed-loop input-output signal gain Af(s) can be expressed in terms of A(s) and 𝛃(s) according to:
|
|
|
(10.1) |
Of
particular interest, one sees from Eqn. (10.1) that that characteristic
equation for a positive feedback system, ![]() , includes a
negative sign.
This
is opposite to what we saw in Chapter 9 for negative feedback systems where the
denominator term includes a positive sign.
, includes a
negative sign.
This
is opposite to what we saw in Chapter 9 for negative feedback systems where the
denominator term includes a positive sign.
As the actual signal sensed by the feedback loop may not be the signal that is designated as the output signal xo(s), an additional signal is introduced called the sense signal, xSen(s). To model the difference between the sense and output signal, an additional 𝛄(s) block is included in the block diagram of Fig, 10.1(b). The input-output relationship of 𝛄(s) can be expressed as follows:
|
|
|
(10.2) |
The closed-loop input-output signal gain Af(s) of the modified single-loop positive feedback structure expressed in terms of A(s), 𝛃(s) and 𝛄(s) is written as
|
|
|
(10.3) |
Here
it is assumed that the zeros of the 𝛄(s) block does not interfere with the zeros
of ![]() , and further, the
poles of 𝛄(s) are assumed to be
in the left-hand plane. Consequently,
the stability behavior of the single-loop positive feedback circuit is
determined exclusively by the zeros of the equation
, and further, the
poles of 𝛄(s) are assumed to be
in the left-hand plane. Consequently,
the stability behavior of the single-loop positive feedback circuit is
determined exclusively by the zeros of the equation ![]() .
.
The
intermediate signals of the single-loop positive feedback are designated as the
feedback and regeneration signal, xFdbk(s) and xRegen(s), respectively. While the reader would already be
familiar to the feedback signal, i.e., xFdbk(s) =![]() , the regeneration signal xRegen(s) is the negative of the error signal
of a negative feedback systems. Thus, the regenerated signal xRegen(s) is defined as the sum of the input
and feedback signals given by
, the regeneration signal xRegen(s) is the negative of the error signal
of a negative feedback systems. Thus, the regenerated signal xRegen(s) is defined as the sum of the input
and feedback signals given by
|
|
|
(10.4) |
Conversely, the above equation can be rearranged to suggest that the difference between the regeneration and feedback signals must equal the input signal, i.e.,
|
|
|
(10.5) |
|
Fig. 10.2: Illustrating the intermediate transfer functions from input to feedback variable (TRegen(s), TFdbk(s) and TSen(s) and the input-output transfer function To(s). |
10.1.1 Parameters of a Single-Loop Positive Feedback System
Since Chapter 8 was devoted to the parameterization of single-loop negative feedback systems, one can follow the same approach given there and apply it to the single-loop positive feedback structure of Fig. 10.1(b). As such, one can immediately identify the feedback parameters A(s), β(s) and 𝛄(s) as the ratio of the following of the intermediate transfer functions:
|
|
|
(10.6) |
|
|
|
(10.7) |
and
|
|
|
(10.8) |
Here the intermediate transfer functions (IFs) are defined as per Fig. 10.2 as
|
|
|
(10.9) |
|
|
|
(10.10) |
and
|
|
|
(10.12) |
The input-output transfer function To(s) is defined as
|
|
|
(10.13) |
The intermediate transfer function ratios are almost identical to those given in Chapter 8, with xRegen(s) substituted for xErr(s), and the appropriate sign accounting for an addition operation rather than a subtraction operation. The latter representation is important as positive feedback oscillators rely on regeneration to maintain self-oscillations rather than a cancellation that goes towards a zero state.
|
(a)
|
(b)
|
|
Fig. 10.3: Two ways to identifying the intermediate feedback voltage variables of an arbitrary single-loop positive feedback circuit implementing a voltage-mixing/voltage-sensing topology. (a) Case 1, and (b) Case 2. |
|
10.1.2 Selecting intermediate Feedback Variables for Input Mixing Compliance
At the heart of the parameter isolation method is proper selection of the intermediate feedback variables, xFdbk(s) and xRegen(s) so that the mixing process associated with a single-loop positive feedback circuit is compliant. Mathematically, compliance means that the input and feedback variables must be selected so that Eqn. (10.5) is satisfied. In the case of a voltage mixing topology, the difference between the regeneration and feedback voltage signals must equal the input voltage signal, i.e.,
|
|
|
(10.14) |
This suggests that a KVL loop
formed around the input voltage signal should be divided into two parts, one
being identified as the regeneration voltage signal, and the other as the
negative of the feedback signal. This is depicted in Fig. 10.3(a). Here one
sees the KVL equation for the loop at the front-end of the amplifier
highlighted in red satisfies Eqn. (10.14). One could flip the roles of the
feedback and regeneration signal, together with their signs, as shown in Fig.
10.3(b) and continue to maintain compliance. While the feedback parameters ![]() and
and
![]() will be different, they will have
the same roots of the expression
will be different, they will have
the same roots of the expression ![]() .
.
|
(a)
|
(b)
|
|
Fig. 10.4: Two ways to identifying the intermediate feedback current variables of an arbitrary single-loop positive feedback circuit implementing a current-mixing/voltage-sensing topology. (a) Case 1, and (b) Case 2. |
|
In the case of a current-mixing topology, the difference between the regeneration and feedback current signals must be equal the input current signal, i.e.,
|
|
|
(10.15) |
This suggests that applying KCL at
the feedback node closes to the input signal should consists of three current
components; one would be the input current signal, and the other two would be
assigned the regeneration and feedback current signals. The two possible
arrangements for an arbitrary current-mixing/voltage-sensing circuit are
provided in Fig. 10.4. Here the node that is mixing the input signal with the
feedback current variables, ![]() and
and ![]() , is identified with a red circle.
Writing KCL at this node verifies that the Eqn. (10.15) is indeed satisfied.
, is identified with a red circle.
Writing KCL at this node verifies that the Eqn. (10.15) is indeed satisfied.
10.1.3 Selecting Sense Variable for Output Compliance
The circuit variable which the circuit senses is either a node voltage or branch current, as the choice is somewhat arbitrary. However, it is paramount that the sense variable is located directly on the circuit path of the feedback loop. Any circuit variable not on the path of the feedback loop cannot be sensed and be used to provide corrective action. In some circumstances, the sense variable is not equal to the designated output. This is depicted in the circuits of Fig. 10.4. The amplifier voltage output is designated as the sense signal, whereas the voltage across impedance Z5 is designated as the circuit output. Clearly, this voltage is not on the feedback path of the circuit.

Table 10.1. Nyquist Stability Criterion for positive or regeneration feedback systems.
10.2 Loop Gain Condition for Oscillation – Nyquist Stability Criterion
The loop transmission function ![]() of
an oscillator can be expressed in term of the IFs by combining Eqns. (10.6) and
(10.7) as
of
an oscillator can be expressed in term of the IFs by combining Eqns. (10.6) and
(10.7) as
|
|
|
(10.16) |
We shall denote this product more simply as ![]() .
As the roles of the feedback and regeneration variables can always be interchange,
there are always two ways to express the loop transmission function. The
designation will depend on whether the ratio
.
As the roles of the feedback and regeneration variables can always be interchange,
there are always two ways to express the loop transmission function. The
designation will depend on whether the ratio ![]() is
proper or improper. Collectively, one can summarize this as follows
is
proper or improper. Collectively, one can summarize this as follows
|
|
|
(10.17) |
Similar expression can be applied to both the ![]() and
and
![]() terms.
These are not shown here.
terms.
These are not shown here.
Using the same reasoning as Nyquist, the poles of the closed-loop gain Af(s) of a single-loop positive feedback system can be identified to be in either the LHP or RHP of the s-plane using the Cauchy’s principle of argument of complex functions. As the characteristic equation of the closed loop positive feedback system is 1 – A(s)β(s) as opposed to 1 + A(s)β(s) the rules of encirclement of the critical point still applies, albeit the critical point is now 1+j0. All other rules described for the Nyquist Stability Criterion earlier in Chapter 9 apply the same way. It is only the critical point that has moved. This formulation of the stability criterion for positive feedback systems is in fact the manner in which Nyquist first presented his stability theory [Nyquist,1932].
Recall from Chapter 9 that the principle of argument of complex functions applied to the open-loop system Aβ(s) leads to the following conclusion about the RHP poles of the closed-loop system,
|
|
|
(10.18) |
where ![]() is
the number of RHP poles associated with the closed-loop system and
is
the number of RHP poles associated with the closed-loop system and ![]() are
the number of RHP poles associated with the open-loop system
are
the number of RHP poles associated with the open-loop system ![]() .
The term
.
The term ![]() represents
the number of times the critical point of +1+j0 is encircled in a clockwise
direction. It is important to recognize the condition of the nature of the
open-loop transfer function Aβ(s) as whether it is proper
or improper transfer function, otherwise numerical issue will arise. A proper
transfer function is one where the numerator order is equal to or less than its
denominator order. An improper transfer function is one where the numerator
order is greater than the denominator order. Table 10.1 summarizes the Nyquist
Stability Criterion for positive feedback or regeneration systems as it applies
to proper and improper loop gain transfer functions.
represents
the number of times the critical point of +1+j0 is encircled in a clockwise
direction. It is important to recognize the condition of the nature of the
open-loop transfer function Aβ(s) as whether it is proper
or improper transfer function, otherwise numerical issue will arise. A proper
transfer function is one where the numerator order is equal to or less than its
denominator order. An improper transfer function is one where the numerator
order is greater than the denominator order. Table 10.1 summarizes the Nyquist
Stability Criterion for positive feedback or regeneration systems as it applies
to proper and improper loop gain transfer functions.
10.3 The Wein-Bridge Oscillator
Oscillators occur in nature and in man-made systems. Their behavior is characterized by amplitude and frequency. Their behavior is driven almost exclusively by the second law of thermodynamics which states that the energy of a system tends to a minimum at its equilibrium. Autonomous oscillators, such as the ones we are investigating here, are non-linear oscillating systems that draw its energy from the power supply. The idea that an oscillator is a linear system with poles placed exactly on the j-omega axis is a falsity. While a system may oscillate when its poles are on the j-omega axis, this is not a robust design strategy as any change in the system components will cause the poles to move; thus, influencing its oscillating behavior. Think of balancing a football (soccer ball) on the end of a 6-foot-long pole. While this can be done, any disturbance will cause the ball to fall off and change its point of equilibrium. Consequently, oscillators are designed so that the linearization of the small-signal circuit has its poles in the RHP. This allows the thermal noise of the circuit to start the oscillation build up. However, to counter the positive flow of energy into the circuit from the power supply, at higher signal amplitudes, the circuit switches into a new topology that must dissipate this energy so that the energy-in equals the energy-out over a period of oscillation. To do so, the linearized equivalent circuit of the large-signal circuit must have poles in the LHP. One way to do this, is to include a nonlinear circuit for gain control in either the feedforward or feedback paths of the oscillator.
Oscillators may be classified with respect to its waveform as relaxation, sinusoidal, multi-frequency or chaotic. One may classify with respect to application, e.g., used to synchronize systems, as the carrier of a communication system or used to a probe signal to test a system (instrumentation). One may also classify with respect to implementation, e.g., voltage controlled (VCO), integrated or lumped element. Over the rest of this chapter, several popular oscillator circuits will be investigated using the parameter isolation method.
|
(a)
|
|
|
(b) |
(c) |
|
Fig. 10.5: (a) The Wein-bridge oscillator circuit with frequency and amplitude control, (b) Small-signal linear representation, and (c) Large-signal linear representation. |
|
|
Fig. 10.6: The LTSpice captured schematic diagram of the Wein-Bridge amplifier assuming a shunt-mixing approach. Here the operational amplifier is replaced by a voltage-controlled voltage source having a voltage gain of 106 V/V. The input is excited with a 1-A AC signal. The shunt mixing signals are monitored using three individual 0-valued voltage sources. The polarity of these source defines the reference current direction.
|
10.3.1 A Shunt-Mixing Perspective of the Wein-Bridge Oscillator
An example of a sinusoidal oscillator topology is the Wein-Bridge oscillator shown in Fig. 10.5(a). The frequency of oscillation of the Wein-Bridge oscillator is given by the following expression:
|
|
|
(10.19) |
The diode limiter included in the feedback path around the op-amp limits the gain of the feedforward path when the signal amplitude is greater than, say 0.7 V. Signal amplitude below 0.7 V, the diodes are assumed open-circuit and the gain of the feedforward path is set by R3 and R4 alone (see Fig.10.5(b)). However, when the signal amplitude is greater than 0.7 V, the diode conducts and resistor Rlimit is placed in parallel with R4 (see Fig. 10.5(c)), thus reducing the gain in the feedforward path. The objective of any oscillator design is to place the poles of the linear equivalent representation of the oscillator circuit (i.e., small-signal approximation) in the RHP so that small noise effects will kick-start the oscillation cycle. To prevent the output from growing without bound, the gain in the feedforward signal path reduces and the oscillator begins to dissipate the stored energy thereby obtaining an oscillation equilibrium over one cycle. This is equivalent to the poles of the oscillator circuit moving between the RHP for small-signals and then into the LHP under large signal conditions. Consequently, the instantaneous frequency of oscillation changes over time but the average frequency is equal to that described by Eqn. (10.19).
|
|
Fig. 10.7: The A, 𝛃 and A𝛃 parameters of the Wein-Bridge Oscillator of Fig. 10.4(a) when R4 is set to 25 k-ohms. The plot of A𝛃 reveals a loop gain that has a zero at DC and two LHP poles around 1 kHz.
|
To investigate the Wein-Bridge oscillator, two identical resistors R1 = R2 = 10 kΩ and 2 identical capacitors of C1 = C2 = 16 nF will be incorporated into the design. Together, one can expect an oscillation frequency of approximately 1000 Hz. The noninverting amplifier incorporated into the design will be set to have a gain of 3.5 V/V by using resistors R3=10k ohm and R4= 25k ohms. The limiter resistor Rlimit will be assigned a 100 kΩ value. The two anti-parallel diodes will be modeled based on the 1N4148 signal diode. To investigate the small signal behavior of the oscillator, consider the LTSpice circuit schematic shown in Fig. 10.6. Here the oscillator is assumed to be using a current-mixing approach, so three 0-valued voltage sources with the appropriate polarity is incorporated into the circuit to monitor the feedback and regeneration current signals. The operational amplifier will be assumed to have a voltage gain of 106 V/V for all frequencies. An AC analysis from 1 Hz to 100 MHz was performed and the feedforward block A(s) and feedback parameter β(s) have been identified in Fig. 10.7. In addition, the Aβ(s) loop transmission has been plotted with respect to frequency. As is evident from this plot, a single zero is present at DC, as the gain rises at +20 dB/dec. Subsequently, the gain rolls off at -20 dB/dec around 1 kHz as well as its phase, suggesting the presence of two LHP poles at 1 kHz. Mathematically, the loop transmission Aβ(s) can be approximately described as follows
|
|
|
(10.20) |
where k is an arbitrary constant. It is clear that Aβ(s) does not have any poles in the RHP and takes on a proper form.
|
|
|
|
Fig. 10.8: The Nyquist plot for the Wein-Bridge oscillator of Fig. 10.4(a) with R4=25k ohms. Here the critical point of (+1,0) is clearly encircled suggesting its closed-loop poles are in the RHP. |
Fig. 10.9: The Nyquist plot for the Wein-Bridge oscillator of Fig. 10.4(a) with R4 equal to 15k, 20k, 23k and 25k ohms. Here the critical point of (+1,0) has been added to identify the value of R4 that forces the poles in the RHP. |
Converting the loop gain frequency plot to a Nyquist plot, one simply right clicks the left most vertical axis (magnitude vs. frequency) and selects the Nyquist plot instead of the Bode plot. On doing so, one generates the plot shown in Fig. 10.8. Also included in this plot is the complex conjugate of the loop transmission. This is necessary to complete the Nyquist procedure. Superimposed on thus plot is the critical point +1+0j. As mentioned above, there are no open loop RHP poles, so the number of times the Nyquist plot encircles the critical point +1+j0 in a counter-clockwise direction is equal to the number of closed-loop poles in the RHP. As can be clearly seen from the Nyquist plot of Fig. 10.8, the critical point is encircled at least once. As the Nyquist plot for negative decreasing frequencies overlaps the Nyquist plot for positive increasing frequencies (this can be seen by plotting each segment separately), there are in fact two encirclements suggesting that there are two closed-loop poles in the RHP.
It is interesting to see how the Nyquist contour varies with noninverting amplifier gain ranging from 2.5 V/V to 3.5 V/V. This is achieved by setting resistor R4 to the following four values: 15 kΩ, 20 kΩ, 23 kΩ and 25 kΩ. The Nyquist results are shown in Fig. 10.9. Clearly, when the gain is below 3 V/V (R4=20 kΩ), the closed-loop poles of the oscillator remain in the RHP. However, above 3 V/V, with R4 = 20 kΩ, the closed-loop poles move into the RHP. These results are confirmed by the transient results of the oscillator when subject to an initial node voltage of 1.0 V. As the circuit model does not include any noise, an initial node condition is used using the following .IC command; without this, the circuit will not oscillate:
.IC V(IN) = 1.0V
|
|
|
|
|
|
|
|
Fig. 10.10: The transient response of the oscillator with the input node initialized to 1.0 V using the .IC command subject to four different amplifier gains settings: (a) R4 = 15k ohms and, (b) R4 = 20k ohms, (c) R4 = 23k ohms, and (c) R4 = 25k ohms. The fact that when R4 is less than 20k ohms, oscillation does not occur is consistent with Nyquist stability test applied here. When R4 is greater than 20k ohms oscillation is guaranteed and the amplitude is set by the feedback limiter involving the two antiparallel diode connections and Rlimit. With R4 set to 25k ohms the circuit output seems to grow without bound (unsustainable oscillations) |
||
|
|
Nominal R4 = 15k ohms |
Nominal R4 = 20k ohms |
Nominal R4 = 23k ohms |
Nominal R4 = 25k ohms |
||||
|
|
Small Amplitude |
Large Amplitude |
Small Amplitude |
Large Amplitude |
Small Amplitude |
Large Amplitude |
Small Amplitude |
Large Amplitude |
|
Effective R4 |
15k ohms |
15k || 100k = 13k ohms |
20k ohms |
20k || 100k = 16.7k ohms |
23k ohms |
23k || 100k = 18.7 k ohms |
25k ohms |
25k || 100k = 20k ohms |
|
Voltage Gain of Noninverting Amplifier |
2.5 V/V |
2.3 V/V |
3.0 V/V |
2.67 V/V |
3.3 V/V |
2.87 V/V |
3.5 V/V |
3.0 V/V |
|
CL Pole Region |
LHP |
LHP |
RHP (critical) |
LHP |
RHP |
LHP |
RHP |
RHP (critical) |
|
Sustain Oscillation |
No (zero output) |
Yes |
Yes |
No (unbounded output) |
||||
Table 10.2: The small-signal vs. large-signal closed-loop linearized behavior positions for different values of R4 and noninverting amplifier gain.
The results of the transient analysis are shown in Fig. 10.10 for the four different R4 values. For R4 = 15 kΩ, no oscillation is evident as seen in Fig. 10.10(a). When R4 is set to 20 kΩ, a small amplitude oscillation occurs as shown in Fig. 10.10(b). When R4 is set to 25 kΩ, the oscillation amplitude seems to grow without bound as shown in Fig. 10.10(d). Scaling back R4 to 23 kΩ, provides a sustained oscillation with an amplitude of about 1.8 V as shown in Fig. 10.10(c). All this transient behavior can be explained by considering the effective resistance of R4 at small amplitudes of oscillations and large amplitudes of oscillations. Under small-signal conditions, the diodes in the limiter circuit act as open circuits, so that the feedback resistance around the op-amp is R4. However, under large signal conditions, the diodes act as short circuits, placing Rlimiter in parallel with R4; thus, reducing the gain of the noninverting amplifier inside the feedforward signal path. In order to achieve an oscillator with sustained amplitude, both the small and large amplitude system poles must be considered. In fact, the necessary and sufficient conditions of sustained oscillation can be summaries as follows:

Not meeting this condition implies the circuit will not sustain oscillation, i.e., constant non-zero amplitude. Table 10.2 summaries the circuit conditions for four different values of R4 for noninverting gains ranging from 2.5 V/V to 3.5 V/V. The data in this table clearly supports the above statement. Mathematically, one can now state the start-up conditions for the Wein-Bridge oscillator as:
|
|
|
(10.21) |
and its condition for sustain oscillation is:
|
|
|
(10.22) |
It should be clear from the above discussion that the design objective is to place the closed-loop poles of the small-signal linear representation close to the j-omega axis but just inside the RHP, and conversely, place the closed-loop poles of the large-signal linear representation close to the j-omega axis but inside the LHP. The closer these two sets of pole positions can be positioned, the lower the variation in the instantaneous frequency, or phase noise.
|
|
|
Fig. 10.11: The LTSpice captured schematic diagram of the Wein-Bridge oscillator circuit assuming a voltage-mixing positive feedback topology. The input is excited with a 1 V AC signal and the input, feedback and regeneration voltage signals are identified with yellow-highlighted labels. For oscillation to occur, the Fdbk_bar node is initialized at 1 V.
|
|
|
|
|
Fig. 10.12: The A and 𝛃 parameters of the Wein-Bridge Oscillator of Fig. 10.10 with R4=25 kΩ and series-mixing is assumed. Here the A-path has a pole at DC and two LHP zeros around 1 kHz. The beta-path reveals a LHP zero-pole very close to one another but not overlapping. No pole-zero cancelation will occur between A and 𝛃.
|
Fig. 10.13: The loop gain A𝛃 of the Wein-Bridge Oscillator of Fig. 10.8 with R4=25 kΩ when series-mixing is assumed. The plot of A𝛃 reveals a loop gain that has a pole at DC and two finite-value LHP zeros around 1 kHz. |
10.4 A Stability Criterion for an Oscillator Whose Loop Gain Aβ(s) is Improper
In this section, the stability analysis presented in the previous section for the Wein-Bridge oscillator will be repeated here assuming a voltage-mixing positive feedback perspective instead of a current-mixing one. While the conclusions reached in the previous subsection will not change, this situation will highlight an important issue when using the parameter isolation method; that being, loop transmission functions that have an improper transfer function.
Figure 10.11 shows the LTSpice schematic circuit of the Wein-Bridge oscillator with R4=25 kΩ. Here the reference, feedback and regeneration voltage signals of the voltage-mixing arrangement have been identified and highlighted in yellow. An AC frequency analysis was performed, and the feedforward path parameter A(j𝜔) and the feedback path parameter β(j𝜔) have been plotted in Fig. 10.12. Here the A-path has a single pole at DC and two LHP zeros around 1 kHz as demonstrated by the change in slope before and after 1 kHz. The β-path reveals a LHP zero and pole that have essentially cancelled, resulting in essentially a constant gain across frequency. The loop gain Aβ(j𝜔) of the Wein-Bridge oscillator is shown in Fig. 10.13. Mathematically, the loop transmission Aβ(s) can be approximately described as follows
|
|
|
(10.23) |
where k is an arbitrary constant. As is evident Aβ(s) is improper (numerator order is greater than its denominator order) and, hence, the inverse loop transmission function must be used.
|
(a)
|
|
|
(b) |
(c)
|
Fig. 10.14: (a) The inverse of the loop transmission
|
|
To apply this method to the Wein-Bridge oscillator circuit of Fig. 10.11 where the loop gain Aβ(s) was found to be improper, one computes the loop transmission using the inverse ratio of transfer functions, resulting in
|
|
|
|
Here we use the notation ![]() to
signify that the loop transmission function has been inverted.
to
signify that the loop transmission function has been inverted.
Using LTSpice an AC analysis was performed, and a plot of the inverse loop gain is shown in Fig. 10.14(a). The subsequent inverse-Nyquist plot is shown in Fig. 10.14(b) with both the positive and negative portion of the Nyquist contour found using the waveform viewer commands:
|
|
|
|
As is evident, the critical point +1+0j is encircled – in fact twice, one for the positive imaginary values of s and one for the negative imaginary values. While the direction is not shown in the plot, breaking the AC analysis down into small frequency steps reveals that the inverse-Nyquist contour has a clockwise direction for increasing value of imaginary value of s. Thus #Nencirle,inverse = 2.
As the number of RHP zeros in the open-loop system Aβ(s) is zero (albeit there are 2 LHP zeros), Eqn. (10.25) reveals that the closed-loop system will be unstable with 2 poles in the RHP. It is interesting to see how the inverse-Nyquist contour varies with noninverting amplifier gain ranging from 2.5 V/V to 3.5 V/V. This is achieved by setting resistor R4 to the following four values: 15 kΩ, 20 kΩ, 23 kΩ and 25 kΩ. The Nyquist results are shown in Fig. 10.14(c). Clearly, when the gain is below 3 V/V (R4=20 kΩ), the closed-loop poles of the oscillator remain in the RHP. However, above 3 V/V, with R4 = 20 kΩ, the closed-loop poles move into the RHP. This is exactly what was found early in subsection 10.2.1 using the current-mixing approach. This leads one to conclude the voltage-mixing and current-mixing approaches will lead to the exact same results.
|
|
|
|
(a) |
(b) |
|
Fig. 10.15: The Colpitts oscillator circuit: (a) core oscillator circuit, and (b) with amplitude stabilization. |
|
10.5 The Colpitts Oscillator Circuit
The Colpitts op-amp-based oscillator shown in Fig. 10.15(a) is similar to the Wein-bridge op-amp oscillator but uses a single inductor and two capacitors to form a resonance circuit in the feedback path of the circuit. This circuit was invented by Edwin Colpitts in 1918, a Canadian by birth, who later emigrated to the USA to work for Western Electric. While an op-amp configurated as an inverting amplifier is used as part of the Colpitts oscillator in Fig. 10.15(a), other amplifier circuits can be used such as a single-stage BJT or MOSFET amplifiers. The Hartley oscillator which pre-dates the Colpitts oscillator was invented in 1915 is its dual circuit; the resonant circuit uses a single capacitor and two inductors. Fewer inductors are considered an advantage. The frequency of oscillation of the Colpitts oscillator is approximately the resonant frequency of the LC circuit, which is the series combination of the two capacitors in parallel with the inductor, expressed as
|
|
|
(10.24) |
As explain in the previous section for the Wein-bridge oscillator, the start-up or small-signal poles of the oscillator must be placed in the right-half plane in order to establish oscillation. However, to prevent run-away exponential growth, an amplitude stabilization circuit is needed to dissipate the excess energy under large-signal conditions, or, in other words, move the poles into the left-half plane. This is achieved with the addition of resistors R4 and R5 together with diodes D1 and D2 as shown in Fig. 10.15(b).
|
|
|
Fig. 10.16: The LTSpice captured schematic diagram of the Colpitts oscillator circuit with amplitude stabilization assuming a shunt-mixing positive feedback topology. The input is excited with a 1-A AC current signal and the input, feedback and regeneration current signals are identified with yellow-highlighted labels. The current-mixing signals are monitored using three individual 0-valued voltage sources. The polarity of these source defines the reference current direction. The input node IN is initialized using the .IC command to 0 V to ensure the circuit starts with its small-signal operating point. Later, this will be changed to 1 V for large-signal operation.
|
|
|
|
|
Fig. 10.17: The loop gain A𝛃 of the Colpitts Oscillator of Fig. 10.16 under small-signal conditions (.IC V(IN)=0 V) where R2=1.5kΩ and R4=1kΩ. The plot of A𝛃 reveals a loop gain that has a single zero around 100 Hz and a pair of RHP complex zeros around 700 Hz, as another set of LHP complex poles around 500 Hz. A non-finite pole is evident at infinity.
|
Fig. 10.18: The inverse-Nyquist
plot of the small-signal loop transmission |
10.5.1 A Current-Mixing Perspective of the Colpitts Oscillator
To investigate the Colpitts oscillator, two identical capacitor C1 = C2 = 10 𝜇F, an inductor L1 =10 mH and resistors R1 =1 kΩ and R3 =100 Ω will be incorporated into the design. This will provide an oscillation frequency of approximately 711 Hz according to Eqn. (10.24). The op-amp will be of the AD8065 type, selected from the LTSpice component library. In order to establish the gain of the inverting amplifier required for start-up, the feedback resistor R2 will be set to 1.5 kΩ. In addition, to stabilize the oscillator output the feedback limiter circuit involving R4 and R5 will be set to 1 kΩ and 10 kΩ, respectively. The input node IN is initialized using the .IC command to 0 V to ensure the circuit starts within its small-signal operating point by ensuring that the diodes D1 and D2 remain in their off state, i.e.,
.IC V(IN)=0V
Later, this will be changed to 1 V to force it into its large-signal operation. It is important to verify these assumption by performing an operating point analysis using the .OP Spice directive. Here the input and output nodes of the circuit have been pre-labeled using the .OP Data Label so that the operating point can be quickly checked.
Inserting the zero-valued voltage sources as shown in Fig 10.16 to monitor the current-mixing currents, the loop transmission function can be found from
|
|
|
|
From the loop transmission plot, one can identify the poles and zeros and their location in the complex plane. More specifically, from Fig. 10.17 a LHP zero appears around 100 Hz, a pair of LHP poles, most likely complex, appear around 500 Hz and a pair of RHP complex zeros at 700 Hz. Consequently, the following transfer function can be used to describe the small-signal loop gain as
|
|
|
(10.25) |
where k
is an arbitrary constant. As the loop gain transfer function is improper,
the inverse-Nyquist stability criterion is required to judge the behavior of
the oscillator. As the number of RHP zeros associated with Aβ(s) is
equal to 2, then according to Eqn. (10.18), to create an oscillator with 2
poles in the RHP, the number of encirclements of ![]() must be equal to 0, i.e., #Nencirle,inverse
= 0. The inverse-Nyquist plot for the Colpitts oscillator for the
above-described set of component values leads to that shown in Fig. 10.18. As
is evident, the critical point is not encircled, so the closed-loop oscillator
circuit will indeed have two poles in the RHP plane.
must be equal to 0, i.e., #Nencirle,inverse
= 0. The inverse-Nyquist plot for the Colpitts oscillator for the
above-described set of component values leads to that shown in Fig. 10.18. As
is evident, the critical point is not encircled, so the closed-loop oscillator
circuit will indeed have two poles in the RHP plane.
|
|
|
|
Fig. 10.19: The loop gain A𝛃 of the Colpitts Oscillator of Fig. 10.16 under large-signal conditions (.IC V(IN)=1.0 V) where R2=1.5kΩ and R4=1kΩ. The plot of A𝛃 reveals a loop gain that has a single LHP zero around 100 Hz and a pair of LHP complex zeros around 700 Hz, and another set of LHP complex poles around 500 Hz. A non-finite pole is evident at infinity.
|
Fig. 10.20:
The inverse-Nyquist plots of the large-signal loop transmission |
In order to ensure the oscillation does not grow without bound, the large-signal linear operation of the oscillator must have poles located in the LHP. To check this, the initial voltage condition on the input node set by .IC command is increased to 1.0 V, i.e.,
.IC V(IN)=1V
This will force the diodes D1 and D2 to turn on, so that the large-signal linear operation of the circuit can be identified. For large positive output voltage levels, diode D1 will be turned on and R4a will be placed in parallel with R2. Likewise, for large negative output voltage levels, diode D2 will be turned on and R4b will be placed in parallel with R2. Remember to check this condition is met by running a separate DC operating point analysis using the .OP Spice directive command.
To determine which stability criterion applies, the large-signal loop gain behavior Aβ(s) as a function of frequency is shown in Fig. 10.19. As is evident, the loop gain exhibits a LHP zero at 100 Hz, two LHP poles at 500 Hz and a two LHP zeros at 700 Hz. In contrast to the small-signal loop gain behavior, the zeros have moved from the RHP to the LHP. Consequently, to ensure amplitude stabilization, the poles of the large-signal operation must also move into the LHP. According to the inverse-Nyquist stability criterion, the inverse-Nyquist plot must not encircle the critical point. Indeed, as demonstrated in Fig. 10.20, the inverse-Nyquist plot is shown not to encircle the critical point and therefore the poles will remain in the LHP.
|
|
|
|
Fig. 10.21: The transient response of the Colpitts oscillator with two RHP start-up poles and two LHP poles under large-signal conditions: R2 =1.5 kΩ and R4= 1 kΩ with input initial condition of 0 V. |
Fig. 10.22: A comparison of the transient response of the Colpitts oscillator with two different sets of RHP start-up poles: (a) R2=2.5 kΩ, R4= 1 kΩ, and (b) R2=1.5 kΩ, R4= 1 kΩ.
|
Selecting R2 =1.5 kΩ and R4 =1 kΩ and running a transient analysis result in the plot shown in Fig. 10.21. Clearly, a stable output oscillation is evident after the start-up transient is complete. In Fig. 10.22 is a plot of the transient response for two different start-up conditions. In the case when R2=2.5 kΩ, the time for the output to settle into a steady oscillation is much faster than the second condition when R2=1.5 kΩ. This is because the first case condition places the start-up poles at a higher frequency than the second. It is also evident that the amplitude of oscillation has changed.
|
(a) |
(b) |
|
Fig. 10.23: (a) The Pierce oscillator circuit using a CMOS inverter and piezoelectric crystal in the feedback path: (b) Electrical representation of the crystal component in the Pierce oscillator circuit. |
|
10.6 The Pierce Oscillator Circuit using a CMOS Inverter
In contrast to the active-RC oscillators circuit of the previous section, which can attain oscillation stabilities approaching 0.1%, crystal oscillators can obtain frequency stabilities many orders of magnitude greater, on the order of 1 in 106. Furthermore, at the heart of these oscillator circuits is a piezoelectric crystal that forms a resonant circuit with Q factors on the order of 10,000 or more, resulting in highly selective oscillators.
An inexpensive crystal oscillator can be realized with a single crystal and a standard CMOS inverter, with several additional passive components, as shown in Fig. 10.23(a). Such an oscillator is called a Pierce oscillator after its inventor, George Pierce. An equivalent circuit representation of the crystal as part of the Pierce oscillator is shown in Fig. 10.23(b). Here the crystal is model as a compound impedance consisting of two parallel impedance branches. One branch consists of a series RLC circuit involving Rs, Ls and Cs, and the other a single capacitor denoted as Cp. With the crystal inserted into the oscillator circuit, two additional capacitors C1 and C2 appear across the input terminals of the crystal. As these two capacitors are in parallel with Cp of the crystal, when necessary, they can easily be accounted for by replacing Cp with Cp + C1C2/(C1+C2).
As the crystal Q-factor is extremely high, the series resistance Rs can be neglected, and the impedance seen from terminal-to-terminal can be expressed as
|
|
|
(10.26) |
which can be rearranged as follows
|
|
|
(10.27) |
where
|
|
|
(10.28) |
The above impedance function has a zero located at
|
|
|
(10.29) |
and a pole at
|
|
|
(10.30) |
Substituting ws into wp allows one to state
|
|
|
(10.31) |
Piezoelectric crystals are shaped or cut for operation in oscillators to operate under two separate conditions. One where Cp is much larger than Cs so that the oscillator circuit oscillates at the series resonance frequency ws set by the crystal’s series inductance Ls and capacitance Cs. The other is where Cs is much larger than Cp. Regardless of the crystal cut, the frequency of oscillation wo can be bounded between ws and wp according to
|
|
|
(10.32) |
Substituting the above series and parallel resonant frequencies, leads to the following resonant frequency bound:
|
|
|
(10.33) |
|
|
|
Fig. 10.24: The LTSpice captured schematic diagram of the Pierce oscillator circuit. The current-mixing signals are monitored using three individual 0-valued voltage sources. The polarity of these source defines the reference current direction. The crystal is assumed to be cut for series resonance operation.
|
|
|
|
Fig. 10.25: The steady-state response of the Pierce oscillator with Rf =1.0 MΩ and C1=C2=10 pF. The input node was set to 0 V so that initial state of the oscillator was something other than its DC operating point. The oscillation period was found to be 279.277 ns, equivalent to 3.58066 MHz. |
Let us consider operating the Pierce oscillator circuit with a piezoelectric crystal cut for series resonance at 3.579545 MHz. This is the oscillation frequency associated with the NTSC color burst signal used in color television sets. A circuit model of this crystal consists of a series RLC circuit of 50 Ω, 55.5779237 mH and 356.1696 fF, and a parallel capacitance of 8.90 pF. To ensure the oscillation frequency is indeed at the colour burst frequency of 3.579545 MHz, substitute the above component values into Eqn. (10.40) and compute:
|
|
|
|
when simplified, leads to
|
|
|
(10.34) |
To check that these formulas truly bound the frequency of oscillation, an LTSpice simulation was performed using the schematic and device models shown in Fig. 10.24. Here the MOSFETs are model with a level 1 MOS model with |VT|=1 V, 𝜇nCOX = 2 𝜇pCOX =20 𝜇A/V2 and 𝜆=0.04 V-1. Furthermore, the lengths of each transistor are the same at 10 𝜇m and the width of the NMOS and PMOS transistors are 100 𝜇m and 200 𝜇m, respectively. The circuit was initialized with an input voltage of 0 V, so that the circuit has energy to drive the RHP poles. This was performed using the following .IC command,
.IC V(IN)=0V
The results of the transient analysis are shown in Fig. 10.25 under steady-state operation. Over a single period of oscillation, the period is identified to be 279.277 ns, which is equivalent to an oscillation frequency of 3.58066 MHz. This result falls within the frequency bound described above in Eqn. (10.34). To be more precise, however, the oscillation period should be averaged over many individual cycles, as the cycle-to-cycle period does vary over time. This is referred to as cycle-to-cycle jitter.
To demonstrate the insight provided by the frequency bound of Eqn. (10.33), the left-hand side of this expression can be reduced by increasing the load capacitors C1 and C2 to a much larger value. Consider increasing the value of C1 and C2 to 100 pF from 10 pF. Consequently, the frequency bound becomes
|
|
|
(10.35) |
The transient simulation was then repeated, and the frequency of oscillation was extracted. On account of the 20 ns step size set by the .TRAN analysis request, the period was not capable of being resolved any better than that reported in Fig. 10.25. Before venturing down a path to extract the oscillation frequency with greater resolution, we would like to consider a stability analysis to identify how big C1 and C2 can be increased to while ensuring stable operation. To carry this out, we shall maintain Rf at 1 MΩ, R1 at 1 kΩ and the crystal as it was. The load capacitance with C1 = C2, will be swept from 100 pF to 500 pF in increments of 50 pF. Both the loop gain and corresponding inverse-Nyquist plot will be provided to deduce the condition where oscillation stops. It is important to analyze the oscillator around its DC operating point and not the initial operating point used to set up the transient analysis. To achieve this, the input node is initialized at 0 V using the following .IC command,
.IC V(IN)=0V
This command is used to pull the inverter away from its operating point of 2.5 V. Remember to check that the DC operating point is indeed where you want it to be. Here using .OP command the input and output voltage of the amplifier are both found to be equal to 2.5 V.
|
(a) |
(b) |
|
Fig. 10.26: The loop transmission A𝛃 of the Pierce oscillator of Fig. 10.21 under small-signal conditions with R1=1 kΩ and Rf=1 MΩ and load capacitance ranging from 100 pF to 500 pF in 100 pF increments. (a) A wide-ranging view of frequency response loop gain behavior highlighting the zero at DC. (b) An expanded view of the loop transmission response region with complex poles and zeros clearly evident. The magnitude response has been separated from the phase response in order to see the phase action corresponding to the complex pair of zeros.
|
|
The results of the AC analysis reveal the loop gain Aβ(s) as a function of frequency is shown in Fig. 10.26 for five different load conditions ranging from 100 pF to 500 pF in 100 pF increments. The graphs shown in part (a) is a wide-ranging view of the loop gain. Clearly, the loop gain has a finite zero at DC and a non-finite pole at infinity. Subsequently, an improper transfer function would be required to describe the behavior of this loop gain. The graphs shown in part (b) is an expanded view around the series and parallel resonant frequencies. The magnitude response is plotted separately from the phase response so that important details can be seen more clearly. For load capacitance ranging from 100 pF to 400 pF, a complex pair of zeros are located in the RHP, as the phase decreases with increasing magnitude bump. For a load of 500 pF, the pair of complex zeros move into the LHP, as the phase increases with magnitude bump. Consequently, the stability criterion must be adapted to the changing zero locations.
One can also see the effects of the series and parallel resonant frequencies with load capacitance changes in the magnitude plot of Fig. 10.26(b). As the load capacitance increases, both the series and parallel resonant frequencies decrease, with the parallel resonant frequency decreasing at a faster rate. While the latter effect is expected as predicted by Eqn. (10.33), the movement of the series resonant frequency is not predicted by the theory presented earlier. Fortunately, this is a small change and will have a very small effect on the oscillation frequency bound. Nonetheless, the parallel resonant frequency ωp becomes a better estimate of the oscillation frequency under heavy capacitance loads of C1 and C2.
|
|
|
|
Fig. 10.27:
The inverse-Nyquist plots of the loop transmission |
Fig. 10.28: The magnitude and phase response of the closed-loop oscillator Af(s) circuit as a function of load capacitance C1=C2 ranging from 440 pF to 450 pF in the region of the circuit resonance. The sudden change in phase behavior suggest poles moving between the RHP and LHP. For C1=C2=444 pF or less, the complex poles are in the RHP, whereas for C1=C2=446 pF or greater, the poles move into the LHP. |
To investigate the stability of the oscillator, combined with the fact that the loop gain transfer function is improper, i.e., has a zero at DC, the inverse-Nyquist plot is required for the five different capacitance load conditions. In the case of loads of 100 pF to 400 pF, the loop gain reveals 2 complex pair zeros in the RHP. Thus, for oscillation, the inverse-Nyquist plot must not encompass the critical point 1+j0. However, in the case of a load capacitance of 500 pF, one can see from Fig. 10.26(b) that the zeros move over into the LHP. So, to maintain oscillation, the inverse-Nyquist plot should encompass the critical point. An AC analysis was performed, and the inverse-Nyquist plot is displayed in Fig. 10.27. For all five load conditions, the critical point is never encircled. Thus, for loads as high as 400 pF, oscillation will occur. However, for a load capacitance of 500 pF, oscillation will not occur. Somewhere in between 400 pF and 500 pF would be threshold between oscillation and no oscillation. Repeating the previous analysis reveals this threshold to occur around capacitance loads of about 445 pF.
It is interesting to re-confirm these results through a closed-loop analysis of the frequency response behavior of the output of the oscillator circuit. For increasing load capacitance C1 = C2 from 440 pF to 450 pF, a phase shift corresponding to closed-loop poles can be identified. Specifically, in Fig. 10.28, one can see the phase shift in the resonance region of the oscillator corresponding to the poles that moves from the RHP to the LHP, as a pole in the RHP will cause the output phase to increase with increasing frequency and that for a LHP pole with the opposite phase change. Clearly, from Fig. 10.28, the CL poles switch planes midway between C1=C2=444 pF and C1=C2=446 pF. Thus, one can confirm that the inverse-Nyquist analysis indeed predicts the correct results.
|
|
|
Fig. 10.29: The oscillation peak-peak amplitude as a function of the load capacitance C1=C2. As is evident, the amplitude decreases with increasing load capacitance. |
To confirm the results of this frequency domain stability analysis, a transient analysis of oscillator can be conducted for various load capacitance conditions (with initialization). Unfortunately, the amplitude of oscillation decreases rapidly as the load capacitance approaches its critical value of 445 pF as depicted by the plot shown in Fig. 10.29. For capacitive loads above 200 pF, the steady-state oscillation amplitude drops off significantly, making it difficult to see the oscillations when the capacitive loads are greater than 350 pF or more. Consequently, confirming the stability analysis for large load conditions through a transient analysis is difficult to do; largely due to very long simulation times are required. Fortunately, the closed-loop frequency response analysis describe above confirms the validity of the theory presented here. It should be noted though that relying on a closed-loop frequency response to deduce the stability threshold is generally not possible.
10.7 Chapter Summary
· A circuit that incorporates a single-loop positive feedback path can be decomposed into a structure involving a feed-forward block A(s), a feedback block 𝛃(s) and a feed-out block 𝛄(s) as shown below:
· The closed-loop input-output transfer function Af(s) of a single-loop circuit can be expressed in terms of the feedback parameters as follows:
|
|
|
|
· The signals xFdbk, xRegen and xSen are the result of the circuit being driven by an external forcing function xs (either voltage or current), and consequently, three immediate transfer functions can be defined, but only two are independent:
|
|
|
|
|
|
· One additional transfer function can be defined from the input forcing function xs to the output signals, and xo, as follows:
|
|
|
|
|
|
·
The feedback
parameters for the overall feedback structure can be defined in terms of three
intermediate transfer functions, depending on the nature of the transfer
function feedback ratio ![]() :
:
|
|
|
|
|
|
· The loop transmission A𝛃(s) can take on two equivalent forms:
|
|
|
|
|
|
· According to the block diagram of a single-loop positive feedback structure, the input and feedback variables xs, xFdbk and xRegen must satisfy the following equation:
![]()
· If the internal signals (xFdbk and xRegen) involved in the differencing operation are voltage signals, then the feedback action is referred to as voltage-mixing or series-mixing. Conversely, if the mixing signals are currents signals, then the feedback action is referred to as current-mixing or shunt-mixing.
· The sensing signal must be associated with a signal in the feedback loop in order to be output compliant.
· The Nyquist Stability Criterion requires a plot of the loop gain or transmission transfer function on a complex plane Im vs. Re called the Nyquist plot. The stability criterion considers the number of encirclements of the Nyquist plot makes around the critical point of +1+j0.
· According to the Cauchy’s principle of argument for complex functions, the number of RHP poles of the closed-loop system Af(s) will equal to the number of RHP poles of A𝛃(s) plus the number of clockwise encirclements of A𝛃(s) around the critical point +1+j0, i.e.,
![]()
· Consequently, for a circuit to be stable, the number of RHP poles for the closed-loop system must be zero; thus, the number of counter-clockwise encirclements must equal to the number of RHP poles of A𝛃(s), i.e.,
![]()
· The number of encirclements around the critical point required to declare stable closed-loop behavior depends on the number of right half plane (RHP) poles in the loop transmission transfer function.
· For a loop transmission transfer function having no RHP poles (and no pole-zero cancelations) then the Nyquist contour should not encircle the critical point +1+j0.
· Many oscillator circuits make use of single-loop positive feedback topologies.
· Oscillators may be classified with respect to its waveform as relaxation, sinusoidal, multi-frequency or chaotic. One may classify with respect to application,
· Some example oscillator circuits are the Wein-bridge, Colpitts and Pierce, named after their inventors.
· The linearization of the oscillator circuit under small-signal conditions must have at least two poles in the RHP and the linearization of the oscillator circuit under large-signal conditions must have all of its poles in the LHP.
10.7 LTSpice Tips
· A Nyquist plot can be generated with LTSpice – run an AC analysis, select the signals that make up the loop transmission function A𝛃(s) and right click on the magnitude of the vertical axis of the plot that appears, then select the Nyquist plot option under the Bode plot button that appears in the resulting pull-down menu.
· To complete the Nyquist plot, include the complex conjugate of the loop transmission function using the LTSpice operation
|
|
|
|
10.8 Bibliography
H. S. Black, “Stabilized Feedback Amplifiers,” The Bell System Technical Journal, January 1934.
H. Nyquist, “Regeneration Theory,” The Bell System Technical Journal, July 1932.
E. Lindberg, “The Barkhausen Criterion (Observation ?),” 18th IEEE Workshop on Nonlinear Dynamics of Electronic Systems, May 2010.
G. W. Roberts, Microelectronic Circuits, ECSE 334/335 Course Notes, McGill University, 2010 - 2021.
G. W. Roberts, “Single-Loop Feedback Parameter Extraction Method for Stability Analysis of Linear Circuits,” IEEE International Circuits and Systems Conference, Daegu, South Korea, May 2021.
G. W. Roberts, "Identifying A(s) and 𝛽(s) in Single-Loop Feedback Circuits using the Intermediate Transfer Function Approach,” Sensors, vol. 22, 4303, June 2022.
10.9 Problems
10.1 Compare the amplitude of oscillation of the output voltage generated by the Wien-Bridge oscillator shown in Fig. 10.5 with and without the diode limiter in the op-amp feedback path.
10.2 An oscillator is formed by loading a transconductance amplifier having a positive gain with a parallel RLC circuit and connecting the output to the input directly. Let the transconductance amplifier have an input resistance of 10 kΩ and output resistance of 10 kΩ. The LC resonator has L=10 μH, C=1000 pF, and Q=100. For what value of transconductance Gm will the circuit oscillate? Confirm that this value of transconductance does indeed cause the circuit to oscillate. What is the resulting frequency of oscillation?
10.3 Using LTspice, determine the transfer characteristics of the comparator circuit shown in Fig. P10.2. Subsequently, connect a dc source VB=+1 V to the virtual ground of the op-amp through a resistor of RB=10 kΩ and observe that the transfer characteristics are shifted along the vi-axis to the point vi=-(R1/RB)VB. Assume that the op-amp is of the 741 type. Assume that the two diodes have parameters IS=10-14 A and n=1.
10.4 For the circuit in Fig. P10.4, determine the loop transmission A𝛽(jω) and the frequency for zero loop-phase. Verify that the circuit indeed oscillates at this frequency. Assume that the op-amp is of the 741 type.

Fig. P10.2

Fig. P10.4

Fig. P10.5
10.5 For the circuit in Fig. P10.5, plot its input-output transfer characteristics vo-vi using LTspice. Assume that the op-amp is modeled after the 741 op-amp and the two diodes after the commercial diode 1N4148. What is the maximum diode current?
10.6 Consider the circuit of Fig. P10.5 with R1 eliminated and R2 short-circuited. Plot the input--output transfer characteristics. Model the op-amp after the 741 op-amp and the two diodes after the commercial diode 1N4148.
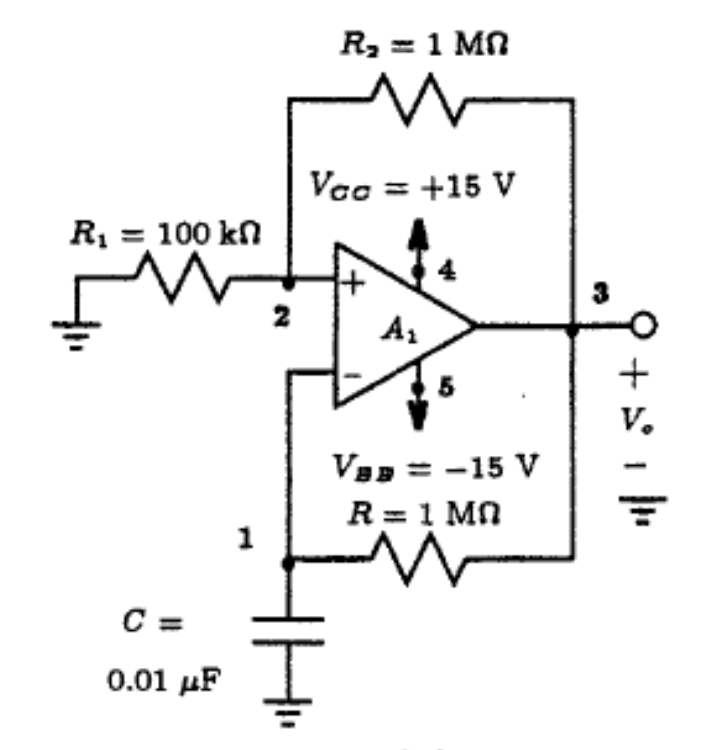
Fig. P10.7
10.7 Find the frequency of oscillation of the circuit in Fig. P10.7 for the case R1=10 kΩ, R2=16 kΩ, C=10 nF, and R=62 kΩ. Assume that the op-amp is of the 741 type.
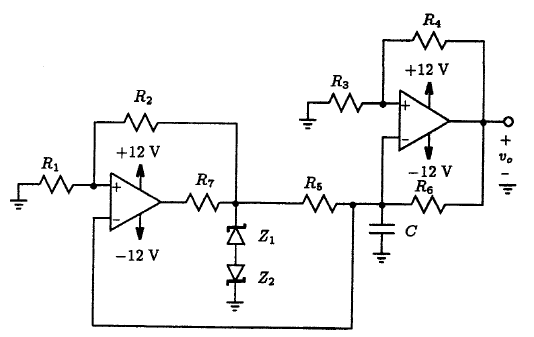
Fig. P10.8
10.8 The circuit of Fig. P10.8 consists of an inverting bistable multivibrator with an output limiter and a noninverting integrator. Using equal values for all resistors except R7 and a 0.5 nF capacitor, design the circuit to obtain a square wave at the output of the bistable multivibrator of 10 V peak-to-peak amplitude and a 10 kHz frequency. Plot the transient voltage waveform appearing at the integrator output. Model the op-amp as a 741-type and the 10-V zener diodes after the BZX84C10L type from OnSemi.
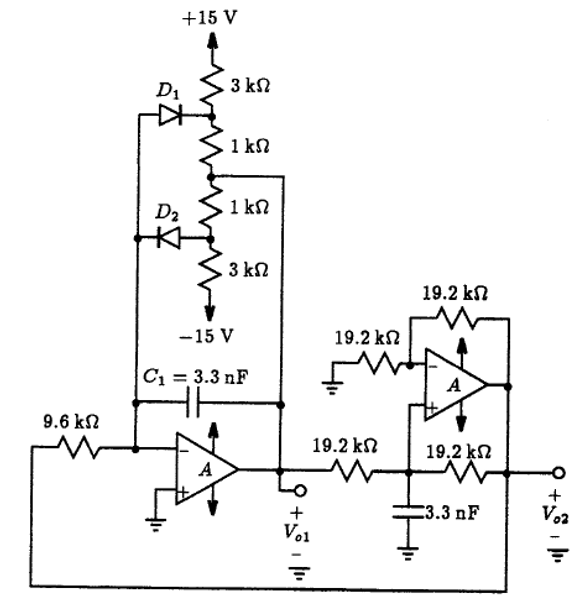
Fig. P10.9
10.9 An oscillator circuit that generates two sinewave signals that are in quadrature is shown in Fig. P10.9. It oscillates at a frequency of 5 kHz. Using LTspice, confirm that the two output signals are indeed in quadrature (ie., 90o apart) and that the frequency of oscillation is 5 kHz. Also, using the Fourier analysis capability of LTspice, determine the total harmonic distortion present in the two output waveforms.

Fig. P10.10
10.10 Using LTspice determine the transfer characteristics of the logarithmic amplifier circuit shown in Fig. P10.10. Assume that the op-amp is of the 741 type and the diode has model parameters IS=10-14 A and n=1.2. Next, apply a 1 V, 1 kHz sine-wave to the circuits input and compute the output voltage waveform. Verify that the output voltage is related to the input voltage signal according to the expression:
![]()
![]()
where VT is the thermal voltage.
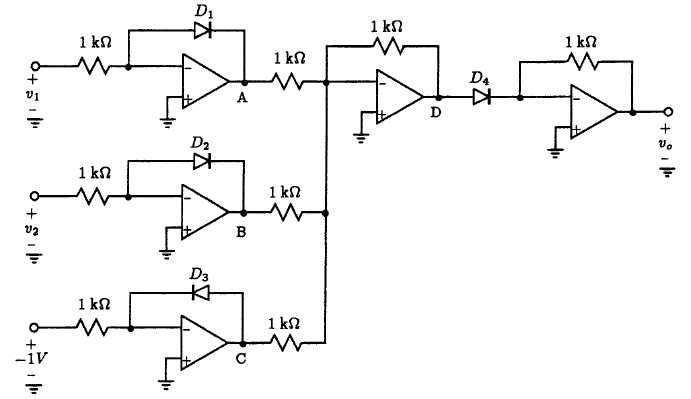
Fig. P10.11
10.11 The circuit of Fig. P10.11 implements the transfer characteristic vo=v1 x v2 for v1 and v2 < 0. Such a circuit is known as an analog multiplier. Using LTspice, determine the transfer characteristics vo - v1 for the following values of v2: 0.1, 0.5, 1.0, 2, 3, 5, 10 V. Assume all diodes to be identical, with 700 mV drop at 1 mA current and n=2. Model the op-amp as a high-gain VCVS with a diode clamping circuit to limit the range of output voltage to ±12 V.
10.12 For the multiplier circuit shown in Fig. P10.11, use LTspice to compute its output voltage waveform vo assuming that the voltage waveform applied to input v1 is described by 1 + 0.001 sin ( 2 π 104 ) V and the voltage signal applied to input v2 is described by 1 + 0.001sin ( 2 π 103 ) V.
10.13 Consider that a squarer circuit can be realized using the multiplier circuit shown in Fig. P10.11 by connecting the two inputs (v1 and v2) together, forming a single input. Apply a 1-volt-peak sinewave of 1 kHz, offset by +5 V, to the input and compute the output voltage waveform for at least one complete period of the output signal. What happens to the output signal if the dc offset voltage is reduced to 0 V?
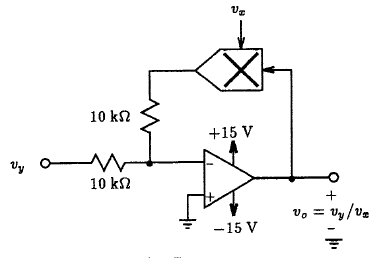
Fig. P10.14
10.14 A circuit that divides one signal by another can be realized using a multiplier circuit such as the one shown in Fig. P10.14 arranged in the feedback loop of an op-amp as demonstrated in Fig. P10.14. The polygon with a cross in the center is meant to symbolize the multiplier circuit shown in Fig. P10.11. Verify the operation of this divider circuit by computing the transfer characteristics vo - vx for the following values of vy: -1, 0.1, 0.5, 1.0, 2, 3, 5 and 10 V.
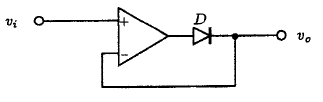
Fig. P10.15
10.15 Two super-diode circuits, such as the one shown in Fig. P10.15, are connected to a common load resistor of 20 kΩ and having the same input signal have their diodes reversed, one with cathode to the load, the other with anode to load. For a sinewave input of 10 V peak to peak and 1 kHz frequency, using LTspice, plot the output voltage waveform and the current supplied by each super-diode circuit. Assume that the op-amp and diode is modeled after the 741 and 1N4148, respectively.
10.16 The super-diode circuit of Fig. P10.15 can be made to have gain by connecting a resistor R2 in place of the short circuit between the cathode of the diode and the negative input terminal of the op-amp, and a resistor R1 between the negative input terminal and ground. Design the circuit for a gain of 2. For a 10 V peak-to-peak input sinewave of 1 kHz frequency, determine, with the aid of LTspice, the average voltage waveform appearing at the output. Assume that the op-amp is modeled after the 741 op-amp and the diode after the 1N4148.

Fig. P10.17
10.17 The circuit shown in Fig. P10.17 is used as a voltmeter which is intended to function at frequencies of 10 Hz and above. It consists of precision half-wave rectifier followed by a first-order lowpass filter. Apply a 100 mV rms sinewave input signal of 10 kHz and observe the voltage signal appearing at the output. Does the output signal correspond to the average value of the input signal? Repeat with a triangular waveform and a square-wave as input. Model the op-amp as a high-gain VCVS with a diode clamping circuit to limit the range of output voltage to ±12 V. Assume that the diode has parameters IS=10-14 A and n=1.6.
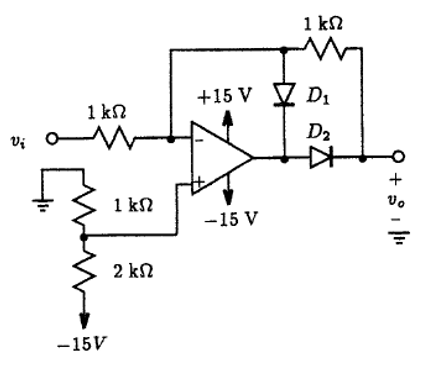
Fig. P10.18
10.18 Using LTspice, plot the transfer characteristics of the circuit in Fig. P10.18. Assume that the op-amp is modeled after the 741 op-amp and the diode after the 1N4148.

Fig. P10.19
10.19 With the aid of LTspice, determine the transfer characteristics vo1 - vi and vo - vi of the circuit shown in Fig. P10.19. Assume that the op-amp is modeled after the 741 op-amp and the diode after the 1N4148.
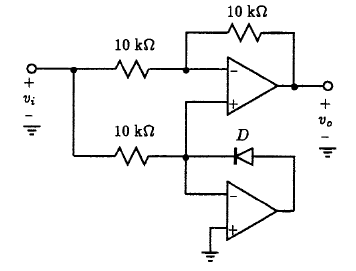
Fig. P10.20
10.20 Using LTspice, plot the transfer characteristics of the circuit in Fig. P10.20. Assume that the op-amp is modeled after the 741 op-amp and the diode after the 1N4148.




















































